PSR of Bandgap Reference
Recently, the performance of the chip I designed in my work got degraded by the insufficient PSRR of a bandgap reference, so I did some investigation about this topic and did some math. Let’s start it.
The method of the calculation basically reference to: https://zhuanlan.zhihu.com/p/696029664 .
If you want me concentrate the whole calculation into one sentence, it would be: cut the feedback loop at the output of the OPA, and figure out the the transfer function(TF) of this node from supply noise, and list the TF from this node to the BG output, then cancels all the variables related to the internal node; in the end, the expression of PSR of BG can be gotten.
Schematic:
A very traditional BG:
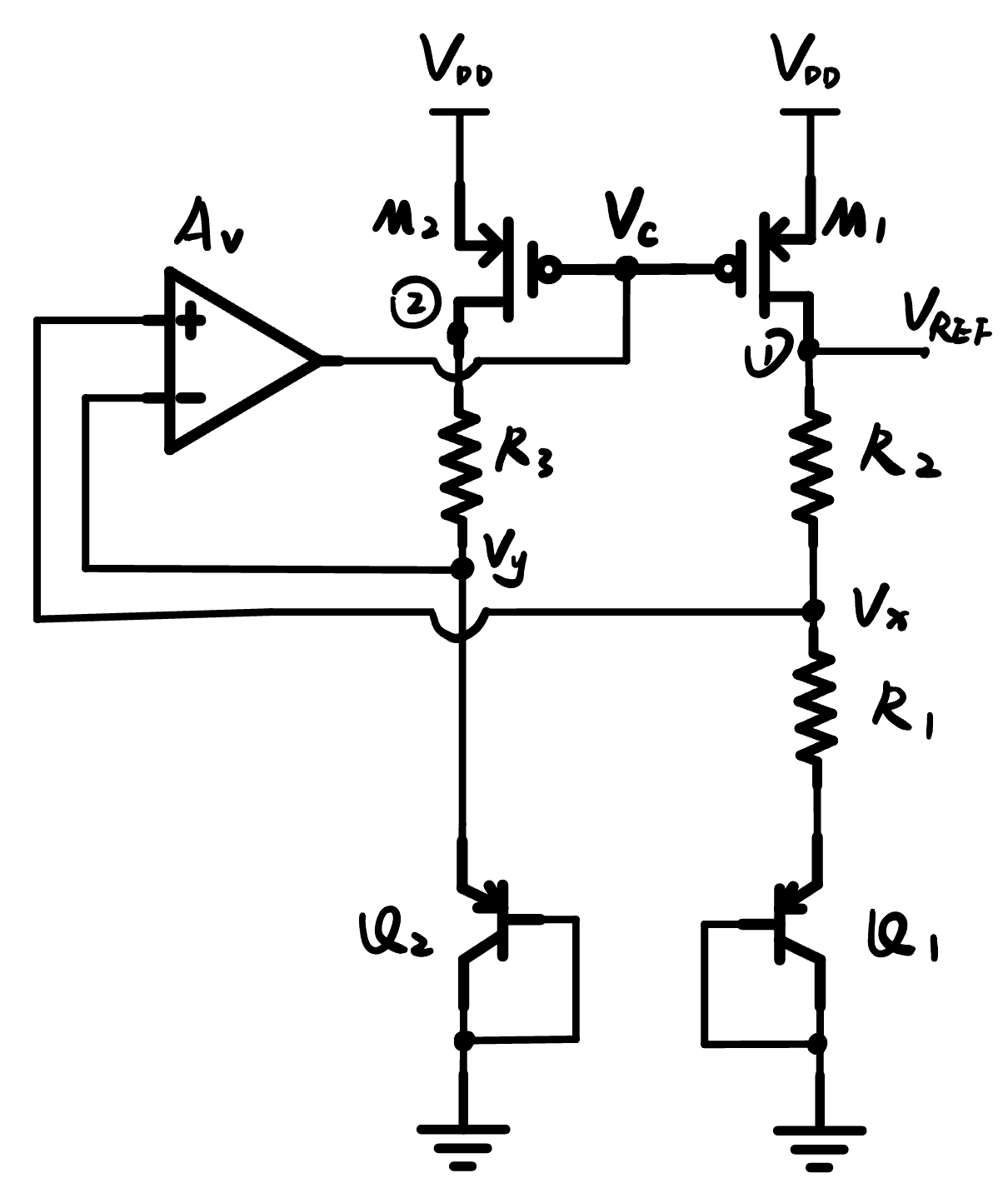
Equations
First thing is some equations:
\[R_{out,1} = r_{o1} //(R_2 + R_1 + R_{Q1}),\] \[R_{out,2} = r_{o2} //(R_3 + R_{Q2}),\]where $r_{o1}$ and $r_{o2}$ are output impedance of PMOS M1 and M2, $R_{Q1}$ and $R_{Q2}$ are the equivalent impedance of two diode-conected PNP BJTs. Therefore, $R_{out,1}$ and $R_{out,2}$ are equivalent impedance seen from node 1 and node 2.
\[v_1 = -g_{mp} \cdot R_{out,1} \cdot v_c + g_{mp} \cdot R_{out,1} \cdot v_{dd} = (v_{dd} - v_c) \cdot g_{mp} \cdot R_{out,1} \ \ ,\] \[v_2 = -g_{mp} \cdot R_{out,2} \cdot v_c + g_{mp} \cdot R_{out,2} \cdot v_{dd} = (v_{dd} - v_c) \cdot g_{mp} \cdot R_{out,2} \ \ ,\]in these two equations, it is assumed that $g_{mp1} = g_{mp2}=g_{mp}$, and the second term of both is derived from the gain of single-stage common-gate amplifier.
\[v_x = v_1 \cdot \frac{R_1 + R_{Q1}}{R_1 + R_2 + R_{Q1}} = v_1 \cdot \beta_1,\] \[v_y = v_2 \cdot \frac{ R_{Q2}}{ R_3 + R_{Q2}} = v_2 \cdot \beta_2,\]where $\beta_1$ and $\beta_2$ are feedback-ratio of two feedback loops.
\[v_c = A_v \cdot (v_x - v_y) + A_{dd} \cdot v_{dd},\]where $A_{dd}$ is PSR of the OPA.
Calculations
Based on equation (5), (6) and (7), it can be derived:
\[v_x-v_y = v_1 \cdot \beta_1 -v_2 \cdot \beta_2 = (v_{dd}-v_c)\cdot g_{mp} \cdot (R_{out,1} \cdot \beta_1 - R_{out,2} \cdot \beta_2)\]Then,
\[v_c = A_v \cdot (v_x-v_y) + A_{dd} \cdot v_{dd} = \frac{g_{mp} \cdot A_v(R_{out,1} \cdot \beta_1 - R_{out,2} \cdot \beta_2)\cdot v_{dd}+A_{dd}\cdot v_{dd}}{1+g_{mp} \cdot A_v (R_{out,1} \cdot \beta_1 - R_{out,2} \cdot \beta_2)} .\]While for the output, it equals $v_1$, so:
\[v_{REF} = v_1 = (v_{dd} - v_c) \cdot g_{mp} \cdot R_{out,1} = g_{mp} \cdot R_{out,1} \cdot v_{dd} \cdot \frac{1-A_{dd}}{1+g_{mp} \cdot A_v (R_{out,1} \cdot \beta_1 - R_{out,2} \cdot \beta_2)},\]if the $R_{out,1} \approx R_{out,2}$ and $A_v »1$, the output would be:
\[v_{REF} = \frac{1}{(\beta_1 - \beta_2)} \cdot \frac{1-A_{dd}}{A_v}.\]Copyright Statement
This article is an Original Work of Bohao, if reprinted, please indicate the source: http:/merenguelee.github.io/2025/08/23/PSR-of_Bandgap-Reference/